Index
Description
In a general sense, Physics studies the laws of the Universe. This broad perspective can be reduced to say that Physics is concerned in the way in which objects move, that is everything which is subjected to the rules of Mechanics. Nowadays, we know at least four different types of Mechanics which are called: Classical, Quantum, Relativistic and Statistical. Each Mechanic applies under a certain regime. Classical Mechanics deals with everyday objects, Quantum Mechanics with very small particles (like electrons), Relativistic Mechanics with very fast particles (whose velocity is close to the speed of light) and Statistical Mechanics with a big number of elements (of the order of the Avogadro's number). The theoretical description of these four Mechanics relies on the Hamiltonian formalism. Moreover, they can be used together, for instance, when the particles are very little and fast, Relativistic Quantum Mechanics is taken into account.
Statistical Mechanics
When many agents are interacting together, they can give rise to peculiar behaviours which can't be reduced to the sum of the characteristics of the single elements making up the system. Such properties emerge as a collective behaviour of all the particles. These are called Complex Systems. To grasp the concept intuitively, the following analogy is useful: the meaning of a word is not given by the sum of the meanings of each letters which make up the word, but it's the result of the "collective behaviour" of them. Again, in Physics, temperature is defined for a gas as a whole and not for a single particle. Thus, Statistical Mechanics can be considered as the mechanics underlying Complex Systems. Due to the high number of agents making up such systems, it is impossible, as well as not so interesting, to determine with arbitrary precision the behaviour of the system components. Indeed, a certain amount of uncertainty, that is of stochasticity or randomness, needs to be introduced in the mathematical formulation of the phenomenon, hence only averaged quantities can be observed. This is the origin of the adjective "Statistical" in the name of the subject.
Nowadays, the research trends in Statistical Mechanics can be divided in two branches: Non-equilibrium and Equilibrium. In the first case, the time evolution of the system is of main interest. Here, the most important quantity is the current, that is the number of particles flowing in the system in a certain direction. Instead, Equilibrium Statistical Mechanics studies systems which have relaxed, that is when, in the long run, their current is null. In this case, the ability of the agents to assume the same value, called magnetisation, against temperature is studied.
When many agents are interacting together, they can give rise to peculiar behaviours which can't be reduced to the sum of the characteristics of the single elements making up the system. Such properties emerge as a collective behaviour of all the particles. These are called Complex Systems. To grasp the concept intuitively, the following analogy is useful: the meaning of a word is not given by the sum of the meanings of each letters which make up the word, but it's the result of the "collective behaviour" of them. Again, in Physics, temperature is defined for a gas as a whole and not for a single particle. Thus, Statistical Mechanics can be considered as the mechanics underlying Complex Systems. Due to the high number of agents making up such systems, it is impossible, as well as not so interesting, to determine with arbitrary precision the behaviour of the system components. Indeed, a certain amount of uncertainty, that is of stochasticity or randomness, needs to be introduced in the mathematical formulation of the phenomenon, hence only averaged quantities can be observed. This is the origin of the adjective "Statistical" in the name of the subject.
Nowadays, the research trends in Statistical Mechanics can be divided in two branches: Non-equilibrium and Equilibrium. In the first case, the time evolution of the system is of main interest. Here, the most important quantity is the current, that is the number of particles flowing in the system in a certain direction. Instead, Equilibrium Statistical Mechanics studies systems which have relaxed, that is when, in the long run, their current is null. In this case, the ability of the agents to assume the same value, called magnetisation, against temperature is studied.
Specific Topics
My research interests focus on both branches of Statistical Mechanics. In the following, you can find a brief description on the problems I'm working on.
Equilibrium SM
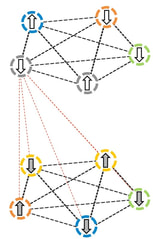
Bipartite Spin Systems
Consider a weighted combination of two lattices (in the case of the picture they are two fully connected graph). If you link the spins of each party of variables in a ferromagnetic or disorder way, you obtain a bipartite spin system. These kind of models present remarkable behaviour, with particular reference to the free energy which gives rise to a degenerate self-consistence equation. The model can be studied also outside the fully connected interaction between the parties, using, for instance, a Bernoulli distributed bond dilution. Moreover, it can be shown that an analogical neural network can be mapped into a bipartite model, widening, in this way, the possible applications of these kind of systems.
References
A. Barra, G. Genovese, F. Guerra
J. Phys. A: Math. Theor. 44 245002 A. Barra, G. Del Ferraro, D. Tantari
EPJB (2013) 86:332 A. Barra, E. Agliari
J. Stat. Mech. (2011) P02027
Consider a weighted combination of two lattices (in the case of the picture they are two fully connected graph). If you link the spins of each party of variables in a ferromagnetic or disorder way, you obtain a bipartite spin system. These kind of models present remarkable behaviour, with particular reference to the free energy which gives rise to a degenerate self-consistence equation. The model can be studied also outside the fully connected interaction between the parties, using, for instance, a Bernoulli distributed bond dilution. Moreover, it can be shown that an analogical neural network can be mapped into a bipartite model, widening, in this way, the possible applications of these kind of systems.
References
A. Barra, G. Genovese, F. Guerra
J. Phys. A: Math. Theor. 44 245002 A. Barra, G. Del Ferraro, D. Tantari
EPJB (2013) 86:332 A. Barra, E. Agliari
J. Stat. Mech. (2011) P02027
Non-Equilibrium SM
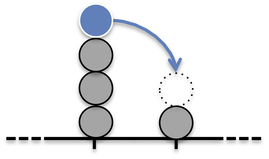
Current Large Deviations
Take a chain in which each site can accommodate any number of particles. The probability of transition between the sites can depend on many parameters and the various models are classified with respect to them. This family of models is often called in the literature as Stochastic Particle Systems. For example, when the probability depends only on the number of particles of the departure site, the model is called Zero Range Process; if it decreases with the number of particles of the arrival site and increases with the number of particles of the departure site, we have the Misanthrope Process. Many properties of SPS have been described in the stationary regime, that is when observation times are large. However, it is also interesting to determine what is the behaviour of these models out of the stationary regime, that is what is the most typical of all the atypical configurations a system can assume. In particular, using the current as a physical observable, it is possible to study these behaviours from a microscopic as well as macroscopic perspective. Theoretical results can be confirmed using numerical simulations techniques stemming from large deviation theory, such as the Cloning Algorithm.
References P. Chleboun, S. Grosskinsky
JSP (2014) 154:432-465 S. Grosskinsky, G. M. Schutz, H. Spohn
JSP (2003) 113:389-410 M. R. Evans, B. Waclaw
J. Phys. A: Math. Theor. 47 095001
Take a chain in which each site can accommodate any number of particles. The probability of transition between the sites can depend on many parameters and the various models are classified with respect to them. This family of models is often called in the literature as Stochastic Particle Systems. For example, when the probability depends only on the number of particles of the departure site, the model is called Zero Range Process; if it decreases with the number of particles of the arrival site and increases with the number of particles of the departure site, we have the Misanthrope Process. Many properties of SPS have been described in the stationary regime, that is when observation times are large. However, it is also interesting to determine what is the behaviour of these models out of the stationary regime, that is what is the most typical of all the atypical configurations a system can assume. In particular, using the current as a physical observable, it is possible to study these behaviours from a microscopic as well as macroscopic perspective. Theoretical results can be confirmed using numerical simulations techniques stemming from large deviation theory, such as the Cloning Algorithm.
References P. Chleboun, S. Grosskinsky
JSP (2014) 154:432-465 S. Grosskinsky, G. M. Schutz, H. Spohn
JSP (2003) 113:389-410 M. R. Evans, B. Waclaw
J. Phys. A: Math. Theor. 47 095001
Optimization
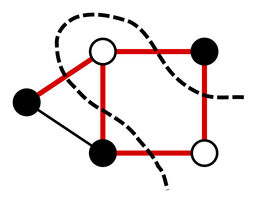
Clustering over Signed Graphs
Consider a network where we associate to each edge a dichotomic variable, i.e. +1 or -1. In this way, we can build a signed adjacency matrix. Allowing the nodes (which in SM are usually called spins) to take +1 or -1 as well, it is interesting to determine the node configuration which maximizes the quadratic form associated to the graph. This can be achieved using many different techniques from Algebra, like spectral analysis, or Physics, like the Ginzburg-Landau functional. In SM this problem can be understood as finding the minimum of the free energy of a disordered system. An important version of this problem is obtained when some values of the nodes are fixed a priori. This simple variation implies the breakdown of standard techniques and requires developing new optimization strategies.
References M. Cucuringu
Journal of Complex Networks, 3 (3):469-506 M. Cucuringu, A. Singer, D. Cowburn
Information and Inference: A Journal of the IMA, 1 (1), pp. 2167 M. Cucuringu, Y. Lipman , A. Singer
ACM Transactions on Sensor Networks, 8 (3), pp. 1-42
Consider a network where we associate to each edge a dichotomic variable, i.e. +1 or -1. In this way, we can build a signed adjacency matrix. Allowing the nodes (which in SM are usually called spins) to take +1 or -1 as well, it is interesting to determine the node configuration which maximizes the quadratic form associated to the graph. This can be achieved using many different techniques from Algebra, like spectral analysis, or Physics, like the Ginzburg-Landau functional. In SM this problem can be understood as finding the minimum of the free energy of a disordered system. An important version of this problem is obtained when some values of the nodes are fixed a priori. This simple variation implies the breakdown of standard techniques and requires developing new optimization strategies.
References M. Cucuringu
Journal of Complex Networks, 3 (3):469-506 M. Cucuringu, A. Singer, D. Cowburn
Information and Inference: A Journal of the IMA, 1 (1), pp. 2167 M. Cucuringu, Y. Lipman , A. Singer
ACM Transactions on Sensor Networks, 8 (3), pp. 1-42